Dynamic Programming

22 Nov 2018

What is Dynamic Programming?

Dynamic programming is a computer programming method where the problem is broken down into smaller sub-problems and solved each sub-problems only once. It is required that those sub-problems overlaps with each other or there exists an optimal substructure. This method was developed in 1950s by Richard Bellman. DP has applications in several fields such as aerospace engineering, economics etc.

When do we apply DP?

There are two main properties of a problem which suggest that the given problme can be solved by using DP. Ther properties are following:

• Overlapping Sub-problems
• Optimal substructure

Overlapping Sub-problems

We use dynamic programming when a solution of a sub-problem is required multiple times. When we find a solution to a sub-problem, we store that solution so that we can use the solution when we find the same problem again. So, DP is not useful if there is no overlapping sub-problems.

Optimal substructure

If it is possible to obtain optimal solution of a problem by using optimal solutions of its sub-problems then we can say that the problem posses optimal substructure property.

Counting n-th Fibonacci Number

Let’s see a program that calculates n-th Fibonacci number in a recursive manner.

/*simple recursive program for Fibonacci numbers*/
int fib(int n){
  if ( n <= 1 )
    return n;
  return fib(n-1) + fib(n-2);
}

Fibonacci Number - Recursion Tree

If we call the previously defined fib() function to generate the 5th number of the Fibonacci series then the function will be executed in a recursive manner. To visualize this understanding we consider the following recursion tree which is generated for the 5th number of the Fibonacci number series.

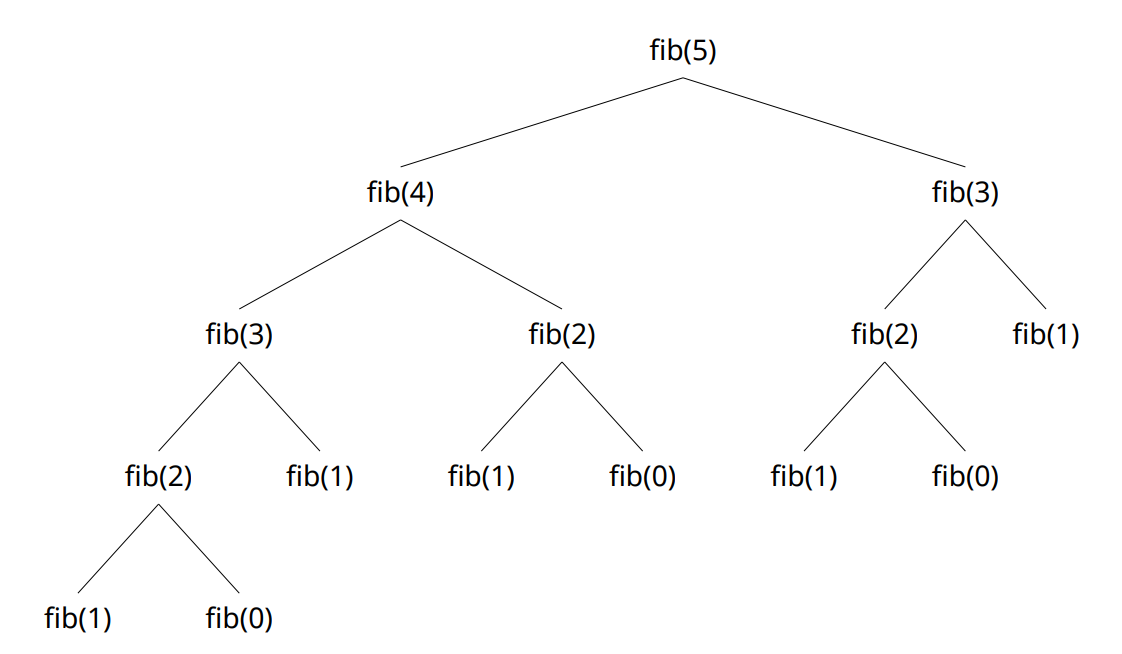
Careful observation of the above tree lead us to find redundant calls to the function fib(). In the above tree, one single function is called several times in a recursive manner.

• fib(0) — 3 times
• fib(1) — 5 times
• fib(2) — 3 times
• fib(3) — 2 times
• fib(4) — 1 time
• fib(5) — 1 time

We don’t want to calculate the value of i-th Fibonacci number if it is calculated once. Instead, we store the result after calculating and use it again when we will need it.

Time complexity for this approach will be exponential which is too costly.

$T(n) = O(2^n)$

Fortunately, there are ways to minimize this cost. We apply DP approach to minimize the cost to calculate Fibonacci series.

Dynamic Programming Approach

There are two types of DP approach that we can follow. They are following.

• Memoization - top down Approach
• Tabulation - bottom up approach

Memoization - Top Down Approach

Memoization is a top down approach. There are reasons why this approach is known as a top down approach. This is a slight modification to the previously defined fib() function. This technique also require recursive calls but stores the result once it is calculated. Then when a function is called we check if it is already calculated or not. If it was calculated before, then we just pass the result or we proceed to calculate.

/* C/C++ program for Memoized version for nth Fibonacci number */
#include<stdio.h>
#define NIL -1
#define MAX 100

int lookup[MAX];

/* Function to initialize NIL values in lookup table */
void _initialize(){
  int i;
  for (i = 0; i < MAX; i++)
  	lookup[i] = NIL;
}

/* function for nth Fibonacci number */
int fib(int n){
  if (lookup[n] == NIL)
  {
  	if (n <= 1)
  		lookup[n] = n;
  	else
  		lookup[n] = fib(n-1) + fib(n-2);
  }

  return lookup[n];
}

int main (){
  int n = 40;
  _initialize();
  printf("Fibonacci number is %d ", fib(n));
  return 0;
}

Tabulation - Bottom Up Approach